Einleitung
Ziel eines Ausgleichungsverfahrens ist es, mit den vorhandenen Daten bestmögliche Koordinaten mit guter Kontrolliertheit zu erzeugen.
Um das Ziel zu erreichen, müssen die eingehenden Standardabweichungen der Bestimmungselemente gut geschätzt werden. Im Auswerteprozess müssen
die in dem Datenmaterial eventuell vorhandenen groben Fehler aufgedeckt und behoben werden. Zum Abschluss eines Verfahrens sollen reale Genauigkeitsangaben
zu den Ergebnisskoordinaten und deren Bestimmungselementen vorliegen.
Um dieses Ziel zu erreichen, muss der Bearbeiter im gesamten Auswerteprozess die Übersicht über die statistischen Ergebnisse behalten. Grobe Fehler
sollten bereits frühzeitig eliminiert werden, da auch sie Messwerte in der Nachbarschaft beeinflussen. Je mehr grobe Fehler in die Berechnung einfließen,
desto schwieriger wird es, die Fehlerursache anhand der erzeugten Ausgabedaten zu lokalisieren.
Im Abschluss eines großen Ausgleichungsverfahrens sollte sich immer die Zeit genommen werden, die Ergebnisse ausgiebig zu analysieren.
Gerade bei schlechten Datengrundlagen, wie es im Liegenschaftskataster in ländlichen Gebieten die Regel ist, ist es oft schwer, grobe Fehler sicher aufzudecken.
Bei schlecht kontrollierten oder korrellierten Daten besteht die Gefahr, dass die erreichten Lagegenauigkeiten nicht der Realität entsprechen.
Um die Ergebnisse richtig zu interpretieren, müssen alle statistischen Angaben zu Rate gezogen werden. Ein fehlerfreier KAFKA-Durchlauf bedeutet nicht,
dass die Ergebnisse der Ausgleichung dieser Zielstellung entsprechen.
Die folgenden Erläuterungen sollen dem Anwender eine Hilfe bei der Interpretation der Statistik geben.
Punkte
Die im Folgenden dargestellten Kennwerte der erzielten Punktgenauigkeit sind im Punktinfodialog einsehbar.
Diesen erreicht man mit dem Werkzeug Markieren entweder durch einen Doppelklick mit der Maus oder im
kontextbezogenen Menü (Rechtsklick) über den Menüpunkt Info.
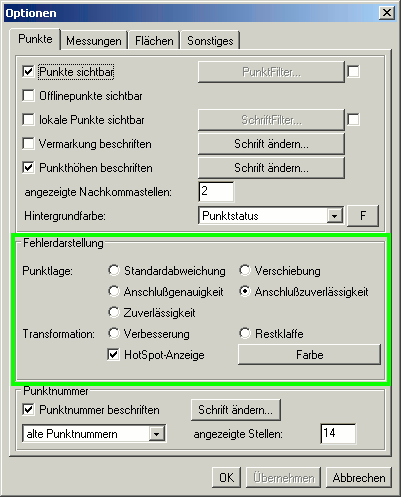
Die Kennwerte können in der KafPlot-Grafik visualisiert werden. Dazu ist in der Symbolleiste der Schalter
Ellipsen  anzuschalten. Unter Ansicht > Optionen > Punkte > Fehlerdarstellung ist der
gewünschte Kennwert anzuwählen. Der Wert wird dann als rote Linie, Ellipse oder Kreis präsentiert. Mit dem Werkzeug
Ellipsen zoomen kann der Maßstab der Fehlerdarstellung beliebig gewählt werden.
anzuschalten. Unter Ansicht > Optionen > Punkte > Fehlerdarstellung ist der
gewünschte Kennwert anzuwählen. Der Wert wird dann als rote Linie, Ellipse oder Kreis präsentiert. Mit dem Werkzeug
Ellipsen zoomen kann der Maßstab der Fehlerdarstellung beliebig gewählt werden.
Um eine visuelle Übersicht über die Statistik zu erhalten, kann die Hotspot-Anzeige angeschalten werden. Die Punkte werden dann anhand der Absolutgröße der jeweils eingestellten Fehlerdarstellung eingefärbt,
kleine Werte erhalten eine grüne Farbe, große Werte eine rote Farbe. Mit Hilfe der Farbwahl Farbe kann die fließende Einfärbung individuell eingestellt werden.
Die Größe der farbigen Hinterlegung kann wieder mit dem Werkzeug Ellipsen zoomen verändert werden.
Soweit die Darstellung der Fehlervisualisierung eingeschalten ist, werden bei der Anwahl von Punkten mit dem Werkzeug Markieren
auch die Größe des gerade visualisierten Kennwertes in der Statusleiste zusätzlich zu den Punktwerten angezeigt.
Koordinatenverschiebung dy, dx und ds
Die Differenz zwischen den ausgeglichenen Koordinaten und den eingegebenen bzw. den durch die nichtredundante Vorausgleichung erzeugten Koordinaten
wird in den Feldern dy und dx gespeichert. Bei beweglichen Anschlusspunkten wird in den beiden Feldern ebenfalls die Differenz zwischen
den ausgeglichenen und den vorgegebenen Anschlusskoordinaten gespeichert. Da bei beweglichen Anschlusspunkten die Koordinatenwerte als zusätzliche Bestimmungselemente
in die Ausgleichung einfließen, werden diese auch in der Statistik des Punktes mit ausgewiesen. Sie werden hier zusätzlich als Verbesserung
in den Koordinatenachsen ausgewiesen. Da die Koordinaten der festen Anschlusspunkte als Konstanten in die Ausgleichung eingeführt werden, werden für
diese Punkte keine Differenzen ausgewiesen.
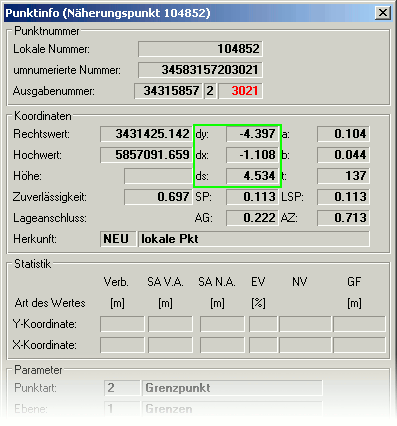
Die Felder dy und dx bei einem Neupunkt
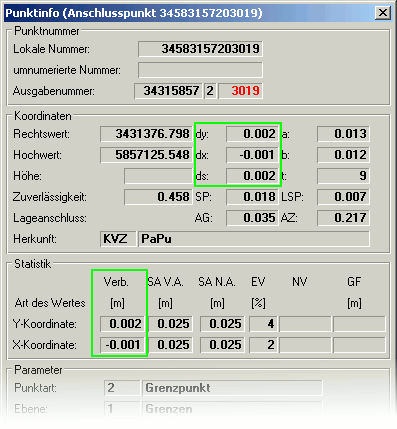
Die Felder dy und dx bei einem beweglichen Anschlusspunkt
KAFKA speichert die Werte für dy und dx in der Ausgabedatei LT3. KafPlot liest aus dieser Datei beide Felder und benutzt die
Werte dy und dx, um nötigenfalls beim Speichern der Auftragsdatei die Ausgangskoordinaten wieder herzustellen. Die Felder dy und dx werden ebenfalls
dazu benutzt, um die Urgeometrie Ansicht > Optionen > Flächen > Urgeometrie anzuzeigen.
Aus den Differenzen in den Koordinatenachsen wird die Länge des Verschiebungsvektors ds ermittelt. Dieses Feld beinhaltet somit die Strecke, um welche sich der Punkt
durch die Ausgleichung verschiebt.
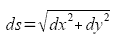
Die vektorielle Anzeige der Punktverschiebung
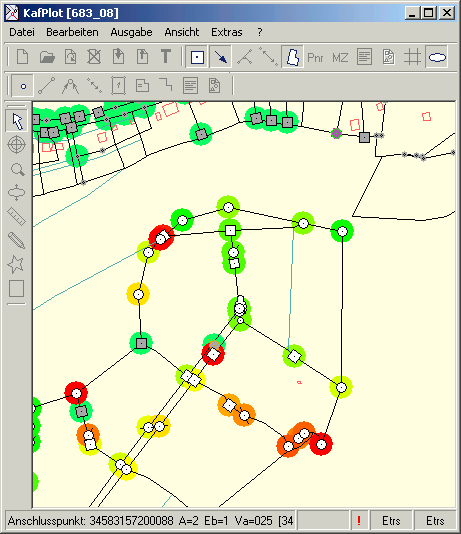
Die Hotspot-Anzeige der Punktverschiebung
Bei der Ausgleichung von flächenhaften Katasternachweis deuten Bereiche mit großen Punktverschiebungen auf eine flächenhafte Verzerrung der Liegenschaftskarte hin.
Dies ist unproblematisch, soweit die Lagerung des Gebietes durch eine ausreichende Anzahl von Passpunkten gestützt ist. Bei einem ungenügendem einseitigen Lageanschluss
kann die Verschiebung eines Gebietes durchaus die Ursache in einem unerkannt fehlerhaften Maß haben. Der Nachweis kann nur über zusätzliche Passpunkte geführt werden.
Soweit nur einzelne Punkte eine von der Umgebung abweichende größere Punktverschiebung aufweisen, ist die Ursache in einem Kartierfehler oder in einzelnen unerkannten Maßfehlern
zu suchen. Mit Hilfe der Punktzuverlässigkeit, dem Grenzwert der Fehlererkennbarkeit GRZW und dem Einfluss eines nicht erkannten groben Fehlers EGK der anliegenden Messwerte ist zu prüfen,
ob ein nicht erkannter Fehler vorliegen kann. Bei schlecht kontrolliertem Katasternachweis kann die Fehlerursache oft nur durch Aufsuchen identischer Punkte
in der Örtlichkeit aufgedeckt werden.
Die Koordinatenverschiebung dy, dx bzw. ds weist die Verschiebung des Punktes gegenüber seiner Ausgangskoordinate nach.
Große Verschiebungen ganzer Punktgruppen ist durch eine ausreichende Anzahl von Passpunkten zu stützen. Bei großen Verschiebungen einzelner Punkte
sind die anliegenden Bestimmungselemente auf einen unerkannten groben Fehler hin zu untersuchen.
Standardabweichung SP, Fehlerellipse a, b und t
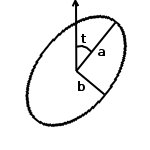
Die Standardabweichung ist ein Maß für die Streuung um den Erwartungswert. Die Standardabweichung SP des Punktes gibt die
erreichte Lagegenauigkeit der ausgeglichenen Punktkoordinaten an.
Für normalverteilte Zufallsgrößen gilt, daß in der einfachen Standardabweichung 68% der Zufallsgrößen liegen.
Innerhalb der zweifachen Standardabweichung liegen 95% der Werte. Die dreifache Standardabweichung stellt sicher,
dass 99% der Werte innerhalb der Fehlerellipsen liegen. Soweit ausgeglichene Punktkoordinaten in die Örtlichkeit übertragen werden oder Fehlergrenzen
dem Endnutzer angegeben werden sollen, ist es üblich, den zwei- oder dreifachen Wert der Standardabweichung anzugeben.
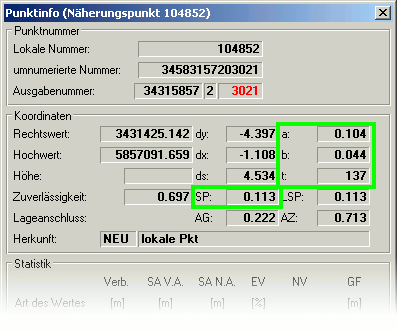
Die Komponenten der Fehlerellipse und die Standardabweichung
KAFKA erzeugt die Komponenten der Helmertschen Fehlerellipse: die große Halbachse a, die kleine Halbachse b und der Richtungswinkel der
großen Halbachse t. Die drei Komponenten werden von KAFKA in die Ausgabedatei LT3 geschrieben, KafPlot liest und verarbeitet diese Werte.
Die Standardabweichung SP errechnet sich aus der Wurzel der Quadratsumme der Halbachsenlänge der Fehlerellipse:
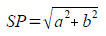
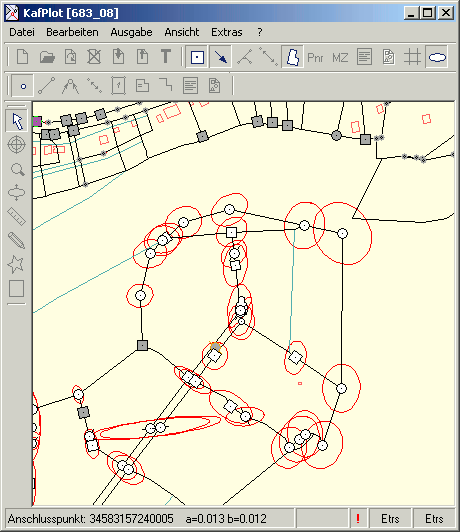
Die Anzeige der Fehlerellipsen
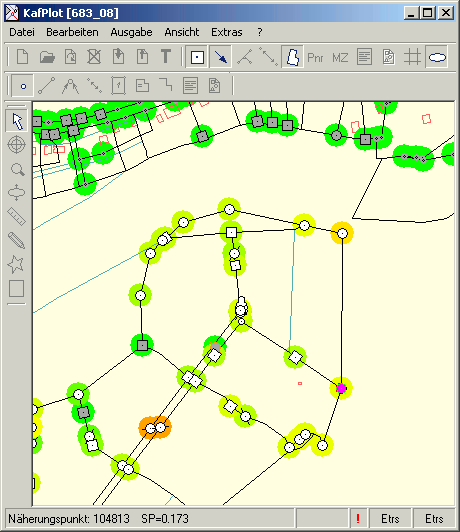
Die Hotspot-Anzeige der Standardabweichung
Die Größe, Form und die Richtung der Fehlerellipse ergibt sich aus der Standardabweichung der Bestimmungselemente und deren Konfiguration.
Die große Halbachse gibt die Richtung der größten zu erwartenden Ungenauigkeit an. So erhalten z.B. einfach polar aufgemessene Neupunkte oft eine Fehlerellipse,
deren große Halbachse quer zur Aufnahmerichtung liegt. Hier ist im Regelfall die Genauigkeit der Richtungsmessung bei größeren Entfernungen geringer
als die Genauigkeit der Streckenmessung. Bei Neuaufnahmen sollte man den Messungsaufbau so gestalten,
dass sich möglichst kreisförmige Fehlerellipsen ergeben.
Bei der Ausgleichung von Messungen kann die Größe und Form der Fehlerellipsen nur durch eine möglichst real geschätzte
Standardabweichung SAV der Bestimmungselemente beeinflusst werden. Ist für Punktgruppen eine ungewünschte Ausbildung der
Ellipsenform zu erkennen, kann eine günstige Auswahl von Passpunkten weiterhelfen.
Die Standardabweichung wird für alle Neupunkte und beweglichen Anschlusspunkte erzeugt, unabhängig davon, wie kontrolliert die Bestimmungselemente sind.
Dass der Wert der Standardabweichung auch der Realität entspricht, kann nur dadurch abgesichert werden, indem die Bestimmungselemente sich gegenseitig genügend kontrollieren.
Theoretisch ist davon auszugehen, dass die Beobachtungen voneinander unabhängig bestimmt und alle groben Fehler aufgedeckt und eliminiert sind. Bei der Auswertung
von historischem Katasternachweis, insbesondere im QL-Verfahren, kann das leider oft nicht garantiert werden. Insbesondere in ländlichen Gebieten mit "dünnem"
Katasternachweis ist es oft nicht möglich, alle groben Fehler aufzudecken. Praktische Erfahrungen zeigen, dass die Ausgleichung hier oft viel
zu geringe Standardabweichungen ergeben, welche einer Überprüfung in der Örtlichkeit nicht standhalten. Die Standardabweichung als wichtigstes Qualitätskriterium der Ausgleichungsrechnung
muss durch eine genügende Zahl von Passpunkten abgesichert werden.
Die Standardabweichung SP kann unter KafPlot verwendet werden, um automatisch eine Lagegenauigkeitsstufe zu bestimmen. Dazu muss in der
Liste Umnummerierung der betreffende Punkt in der Spalte LGA mit einem # markiert werden.
Es kann aber auch ein entsprechender Algorithmus angewendet werden. Unter Extras > Lagegenauigkeitsstufe erzeugen sind
individuelle Einstellungen dazu möglich.
Die Helmertsche Standardabweichung ist ein wichtiges Qualitätskriterium bei der Bewertung der Ausgleichungsergebnisse. Sie gibt die erzielte Lagegenauigkeit
der neu bestimmten Koordinaten in Bezug zu den Anschlusspunkten an. Die Kontrolliertheit der Koordinatenbestimmung geht nicht in die Standardabweichung ein.
Bei der Auswertung von historischem Katasternachweis muss die Bestimmung der Standardabweichung durch eine genügende Anzahl von Passpunkten abgesichert werden.
Lokale Standardabweichung LSP
Die lokale Standardabweichung LSP gibt die Genauigkeit des Punktes in Bezug zu seinen Nachbarpunkten an. Die LSP wird u.a. aus den zum Punkt
gehörigen Beobachtungsverbesserungen und deren Kontrolliertheit berechnet. Neupunkte, die durch unkontrollierte Beobachtungen bestimmt sind,
erhalten im Gegensatz zur Helmertschen Standardabweichung SP keine lokale Standardabweichung LSP. Anhand eines fehlenden LSP-Wertes kann
festgestellt werden, ob ein Punkt unkontrolliert bestimmt wurde.
Soweit Transformationsblöcke mit Restklaffenverteilung berechnet werden, kann KAFKA keine lokale Standardabweichung erzeugen. Diese Information steht dann
nicht zur Verfügung.
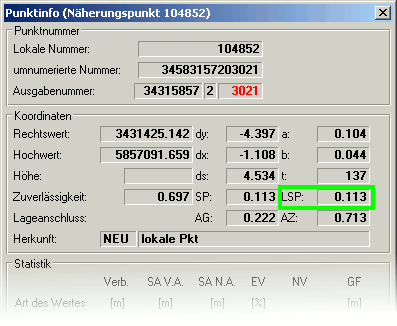
Die lokale Standardabweichung
KAFKA schreibt die lokale Standardabweichung in die Ausgabedatei LT7. KafPlot liest daraus die LSP und ordnet sie dem Punkt zu.
Eine Visualisierung der LSP ist in KafPlot noch nicht möglich.
Die lokale Standardabweichung LSP gibt die Nachbarschaftsgenauigkeit der Punkte an. Die Kontrolliertheit der den Punkt bestimmenden Beobachtungen
gehen in den Wert LSP mit ein. Unkontrolliert bestimmte Punkte erhalten keine LSP.
Zuverlässigkeit ZL
Die Zuverlässigkeit eines Punktes wird aus dem maximalen Einfluss eines nicht erkannten groben Fehlers ( EGK ) der zum Punkt gehörigen Beobachtungen bestimmt.
Sie ist ein Maß dafür, um wieviel sich ein Punkt aufgrund einer unbemerkt grob fehlerhaften Beobachtung in Bezug zu seinen Nachbarpunkten
verschieben könnte. Beobachtungen mit einem geringen Eingangsgewicht (z.B. historischer Katasternachweis) und eine schlechte Kontrolliertheit der Beobachtungen
führen zu einer geringen Zuverlässigkeit.
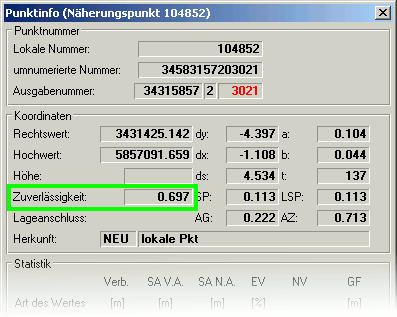
Die Punktzuverlässigkeit
Die Zuverlässigkeit wird von KAFKA nicht berechnet. KafPlot erzeugt diesen Wert anhand der statistischen Werte der Beobachtungen
aus der KAFKA-Ausgabedatei LT2.
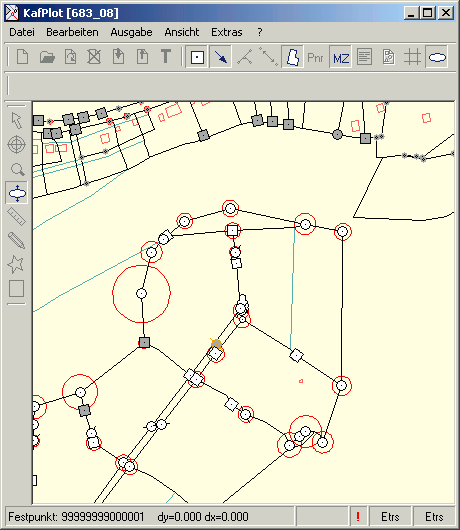
Die Anzeige der Zuverlässigkeit
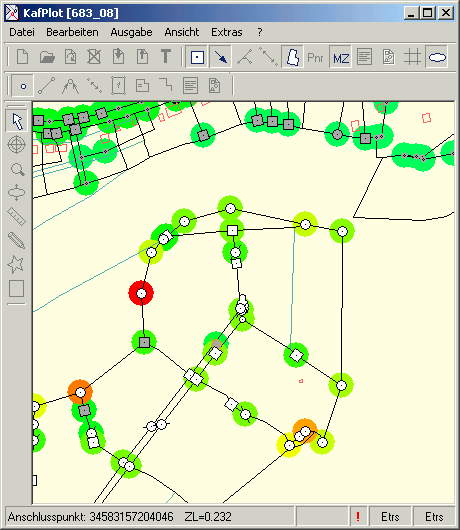
Die Hotspot-Anzeige der Zuverlässigkeit
Soweit sämtliche zum Punkt verfügbaren Beobachtungen in die Ausgleichung eingeführt und deren Standardabweichungen plausibel geschätzt wurden, kann die
Zuverlässigkeit eines Punktes nicht weiter erhöht werden. Die entstehenden Werte müssen letzendlich als gegeben hingenommen werden. Erst wenn sich bei
einer örtlichen Überprüfung Differenzen entgeben, die erheblich die Standardabweichung der Punkte überschreiten, kann die Lagezuverlässigkeit
benutzt werden, um Suchradien einzugrenzen.
Die Zuverlässigkeit ZL ist ein Maß dafür, inwieweit sich ein Punkt aufgrund unerkannt grob fehlerhafter Messungen verschieben kann.
Messungen mit geringer Genauigkeit und Kontrolliertheit erzeugen grobe Werte der Zuverlässigkeit.
Anschlussgenauigkeit AG und -zuverlässigkeit AZ
Testprojekte im QL-Verfahren haben ergeben, dass in Gebieten, in denen die Neupunkte über mehrere verkette Altrisse bestimmt wurden
und keine Passpunkte zur Stützung des Zahlennachweises zur Verfügung standen, die Ausgleichung viel zu genau errechnete Standardabweichungen
ergibt. Dafür gibt es verschiedene Ursachen. Einerseits können bei einer zu geringen Anzahl von Passpunkten die Maßstabsunbekannten der Linienmaßstäbe
nur ungenügend bestimmt werden. Desweiteren können sich bei schlecht kontrollierendem Katasternachweis grobe Fehler kaum aufgedeckt werden, sie fließen vollständig
in die Koordinatenbestimmung ein. Identitätsfehler zwischen verschiedenen Aufmaßen können damit kaum aufgedeckt werden.
Auch Risse mit Punktfeldern, die nur über ein Digitalisiersystem global gelagert sind, erhalten eine für die Örtlichkeit nicht realisierbare zu hohe Genauigkeit,
soweit das Zahlenwerk in sich gut kontrolliert ist.
Diese Umstände lassen sich nur beseitigen, indem weitere Passpunkte in der Örtlichkeit aufgesucht, bestimmt und in die Ausgleichung eingeführt werden.
Um eine Übersicht zu erhalten, an welchen Stellen zusätzliche Passpunkte bestimmt werden müssen, wurde die Anschlussgenauigkeit AG
und die Anschlusszuverlässigkeit AZ der Lage eingeführt.
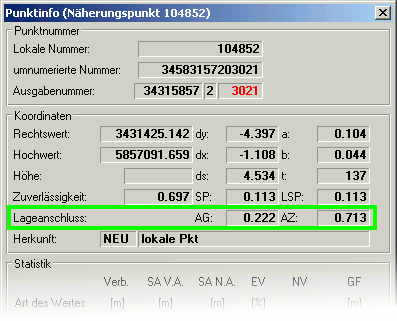
Die Anschlussgenauigkeit und -zuverlässigkeit
Der hierzu von KafPlot verwendete Formelsatz lässt sich wohl kaum wissenschaftlich begründen und soll daher auch hier nicht dargestellt werden.
In der Praxis ergaben sich jedoch realistische Werte. Eingangswerte sind die Standardabweichungen der Beobachtungen und die Normierten Verbesserungen. Bei der
Anschlusszuverlässigkeit wird zusätzlich die Kontrolliertheit der Beobachtungen verwendet.
Die Werte werden iterativ von den Anschlusspunkten auf die Neupunkte übertragen.
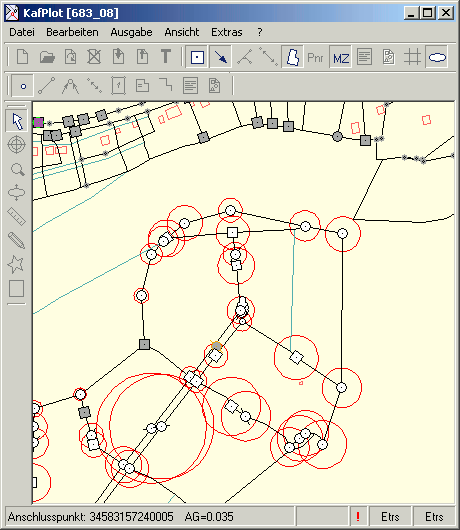
Die Anzeige der Anschlussgenauigkeit
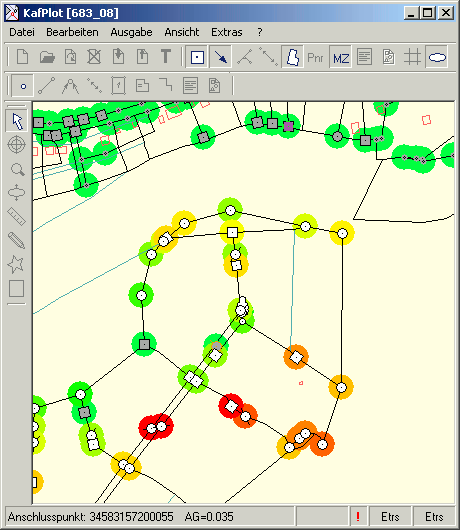
Die Hotspot-Anzeige der Anschlussgenauigkeit
Der Wert der Anschlussgenauigkeit dient als Hilfsmittel zur Beurteilung, in welchen Gebieten zusätzliche Passpunkte bestimmt werden müssen
und wo diese den größten Effekt bringen. Punkfelder, die großflächig schlechtere Anschlussgenauigkeiten ausweisen, sind durch Passpunkte zu stützen.
Die Auswirkung eines Passpunktes in der Nähe der schlechtesten Anschlussgenauigkeit dürfte die größte Wirkung erzielen.
Die Anschlusszuverlässigkeit zeigt eher auf einzelne Punkte, deren Koordinatenbestimmung schlecht kontrolliert sind. Ein an dieser Stelle gemessener Passpunkt
kann zwar grobe Unzuverlässigkeiten aufheben, die Wirkung dieses Passpunktes sich aber nur auf die mit Beobachtungen verknüpften Nachbarpunkte ausweiten.
Die Anschlussgenauigkeit zeigt Werte auf, welche mit wachsendem Abstand zu den Anschlusspunkten immer größer werden.
Bei großflächig schlechten Anschlussgenauigkeiten sollten weitere Passpunkte bestimmt werden. Die Anschlusszuverlässigkeit zeigt Punkte auf, die in Bezug zu den
Anschlusspunkten schlecht kontrolliert berechnet worden sind.
Beobachtungen
Die im Folgenden dargestellten Kennwerte der Beobachtungen sind im Infodialog einsehbar.
Diesen erreicht man mit dem Werkzeug Markieren entweder durch einen Doppelklick mit der Maus oder im
kontextbezogenen Menü (Rechtsklick) über den Menüpunkt Info.
Im Infodialog werden die Kennwerte zu jeder Komponente der Beobachtung angezeigt, im Beispiel für die Komponenten Abzisse, Flucht, Ordinate und Rechter Winkel.
Alle Kennwerte, die eine Dimension besitzen, werden in Meter angezeigt. So werden auch die Verbesserungen und Standardabweichungen von Winkeln in Meter angezeigt (Querfehler).
Im Recorder oder auch bei der Visualisierung werden die Kennwerte der Beobachtung zu einem Wert zusammengefasst.
Je nach Kennwert wird das Mittel oder das Maxima bestimmt.
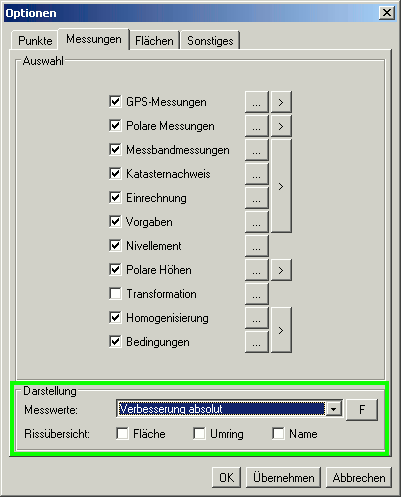
Die Kennwerte können in der KafPlot-Grafik visualisiert werden. Unter Ansicht > Optionen > Messungen > Darstellung ist der
gewünschte Kennwert anzuwählen. Die Beobachtungen (Messungen, Bedingungen, Transformationssysteme) werden dann anhand der Größe des gewählten
Kennwertes eingefärbt. Ein positiv zu wertender Betrag wird im grünen Farbton eingefärbt, negativ zu wertende Größen erhalten einen roten Farbton.
Die Einstellungen zur Einfärbung können zu jedem Kennwert einzeln verändert werden, sie sind unter dem Button F (Farbe) verfügbar.
Bei der Anwahl von Beobachtungen mit dem Werkzeug Markieren
wird auch die Größe des gerade visualisierten Kennwertes in der Statusleiste zusätzlich zu den Beobachtungswerten angezeigt.
Bei eingeschalteter Rissübersicht werden die Rissnamen, Umringe und Flächen je nach gewählten Kennwert eingefärbt. Hier wird der Mittelwert über alle
Beobachtungen des Risses gebildet.
Verbesserung V
Die Verbesserung V ergibt sich aus der Differenz des eingegebenen Messwertes und dem sich aus den endgültigen Koordinaten errechneten Messwertes.

Die Verbesserung
Die Verbesserungen der einzelnen Beobachtungen werden durch KAFKA in der Ausgabedatei LT2 dokumentiert. Soweit das Lesen der LT2-Datei
nicht ausgeschalten ist, liest KafPlot die Verbesserungen und ordnet sie der Beobachtung zu.
Grobe Fehler werden angezeigt, wenn die Verbesserung ca. den dreifachen Wert der Standardabweichung SA VA überschreitet.
Wenn sich nicht mehr akzeptable Verbesserungen ergeben, ohne das ein grober Fehler angezeigt wird, ist die Standardabweichung SA VA
der Beobachtung zu grob geschätzt. Das Gewicht der Beobachtung muss dann erhöht werden.
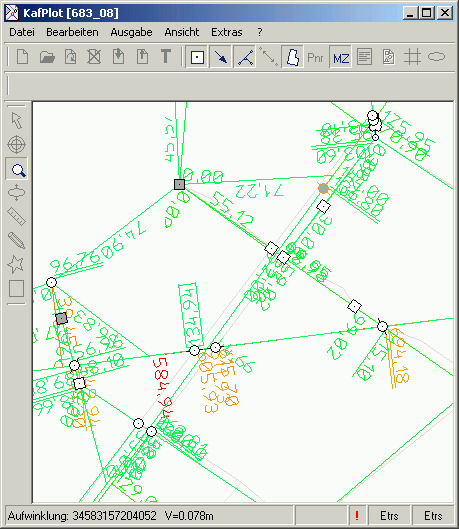
Die Anzeige der Verbesserungen
Die Verbesserung V ist der Betrag, um den ein Messwert verändert wird, um die endgültigen ausgeglichenen Koordinaten zu ergeben.
Standardabweichung SA VA
Die Standardabweichung vor der Ausgleichung SA VA ist die Genauigkeit, mit der die Beobachtung in die Ausgleichung einfließt. Dies ist,
neben den globalen Voreinstellungen in der Steuerdatei, der wichtigste vom Bearbeiter einstellbare Kennwert, mit dem die gesamte Statistik der Ausgleichung beeinflusst wird. Die Standardabweichung
SA VA bestimmt das Gewicht der Einzelbeobachtung bei der Berechnung der Neupunktkoordinaten und ist Ausgangswert für den Test, ob ein
grober Fehler vorliegt.

Die Standardabweichung vor der Ausgleichung
Die in der Regel von der Größe des Messwertes abhängige errechnete Standardabweichung protokolliert KAFKA in der Ausgabedatei LT2.
Soweit das Lesen der Datei LT2 nicht abgeschalten ist, liest KafPlot daraus die Standardabweichungen und ordnet sie dem Messwert zu.
Mit Ausnahme der Transformationsansätze wird die Standardabweichung SA VA für die Beobachtungen global
in den Steuerzeilen für jeden Beobachtungstyp festgelegt. Die einzelne Messung
kann dann mit Gewichten individuell eingestellt werden.
Für die modernen Meßgeräte ist die Standardabweichung der Gerätebeschreibung zu entnehmen. Die Standardabweichungen für historische Messmethoden
entwickelt man am besten aus den zum Zeitpunkt der Messung vorgeschriebenen Grenzwerten. Als Standardabweichung sollte dabei etwa ein Drittel des
Grenzwertes eingestellt werden.
Für Messbandmessungen empfielt es sich, in den Kopfzeilen die Standardabweichungen der aktuellen Vorschriften einzustellen. Historisches
Kataster wird dann, je nach Rissdatum, herabgewichtet. Die in die Ausgleichung eingehende Standardabweichung berechnet KAFKA anhand der Streckenlängen
und multipliziert sie mit der Wurzel des Individualgewichtes.
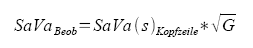
Ein gesamter Riss sollte nur mit einem Gewichtsansatz in der ersten Beobachtungszeile modelliert werden. Individuelle
Gewichtsansätze für einzelne Beobachtungen sollten nur im Ausnahmefall gesetzt werden. Und nur dann, wenn eine plausible Erklärung für eine Herabgewichtung
vorliegt, wie etwa erkennbare Geländegefälle oder Messhindernisse. Es bietet sich aber auch an, einzelne Beobachtungskomponenten unterschiedlich zu gewichten.
So konnten Fluchtungen schon immer mit der heute erreichbaren Genauigkeit in der Örtlichkeit realisiert werden, die Genauigkeit der Messbandmessungen
kann aber auch bei historischen Messungen unterschiedlich sein.
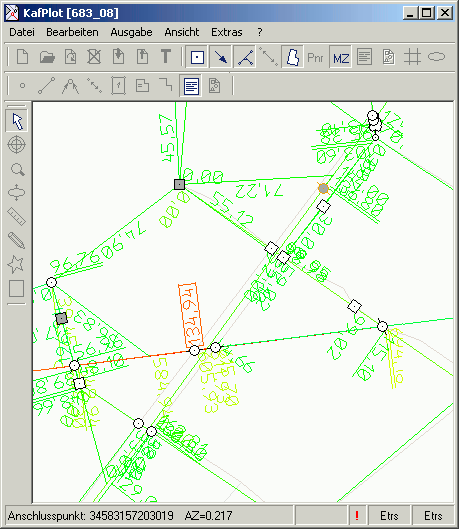
Die Anzeige der Standardabweichungen
Wenn Widersprüche in mehreren Messelementen eines Risses auftreten, liegt es nahe, dass die Standardabweichung der Beobachtungen
zu positiv geschätzt wurden. Hierzu schaltet man in die Anzeige der Normierten Verbesserung NV um. Wenn mehrere Beobachtungen im gelben oder roten Farbton
angezeigt werden, liegen Widersprüche vor. Der Riss wäre in diesem Falle weiter herabzugewichten.
Wird nur für einzelne Messwerte der NV-Wert überschritten, liegt tatsächlich ein Beobachtungsfehler vor. Soweit die Fehlerursache nicht aufgelöst werden kann,
könnte ein Individualgewicht für die Beobachtung gesetzt werden. Damit würde sich ein geringerer Einfluss der Messung auf die Koordinaten ergeben. Allerdings
läuft man dann Gefahr, das falsche Maß herabzugewichten, denn nicht immer zeigt der gröbste NV-Wert die tatsächliche Fehlerursache auf. Bei schlecht kontrollierten
Beobachtungen kann die Fehlerursache oft nicht aufgeklärt werden, hier hilft nur eine Untersuchung in der Örtlichkeit weiter. Inwieweit der Aufwand dafür
gerechtfertigt ist, muss der Bearbeiter anhand der Zielvorgaben selbst entscheiden. Eventuell kann auch der angezeigte Fehler akzeptiert werden.
Die Beobachtung sollte dann nicht herabgewichtet werden, damit auch bei einer späteren Bearbeitung der Widerspruch erkennbar ist. Da aber grobe Fehler nur
wenig Einfluss auf die errechnete Standardabweichung der anhängenden Neupunkte haben, sollten die Punkte entsprechend gekennzeichnet werden,
z.B. in dem sie eine geringere Lagegenauigkeitsstufe erhalten.
Die Standardabweichung vor der Ausgleichung legt den Einfluss der Beobachtung bei der Berechnung der Neupunktkoordinaten fest. Sie hat einen wesentlichen Einfluss
auf die errechneten Standardabweichungen der Neupunkte. Sie wirkt sich auch wesentlich auf die Erkennbarkeit von groben Fehlern aus. Beim dreifachen
Überschreiten der Verbesserung gegenüber der Standardabweichung wird ein grober Fehler angezeigt.
Standardabweichung SA NA
Die Standardabweichung nach der Ausgleichung SA NA ist die Genauigkeit, die sich für die Beobachtung aus der Ausgleichung ergibt.

Die Standardabweichung nach der Ausgleichung
Die sich aus der Ausgleichung ergebende Standardabweichung protokolliert KAFKA in der Ausgabedatei LT2.
Soweit das Lesen der Datei LT2 nicht abgeschalten ist, liest KafPlot daraus die Standardabweichungen und ordnet sie dem Messwert zu.
Leider protokolliert KAFKA diesen Wert nicht für Beobachtungen der orthogonale Linien. Damit ist er nur eingeschränkt nutzbar zur Gesamtbeurteilung
der Ausgleichung. Aus diesem Grund wurde eine direkte Anzeige der SA NA in KafPlot nicht integriert. Angezeigt werden kann die Differenz aus
der Verbesserung V und der Standardabweichung vor der Ausgleichung SA VA.
Die Anzeige der Differenz V - SA VA
Soweit sich für ganze Messgruppen (Risse) hier große Werte ergeben, ist die Standardabweichung zu positiv geschätzt. Eine Herabsetzung
der Beobachtungsgewichte ist angebracht, wenn das schlechtere Ergebnis erklärt werden kann.
Die Standardabweichung nach der Ausgleichung gibt die erzielte Genauigkeit der Beobachtungen nach der Ausgleichung an.
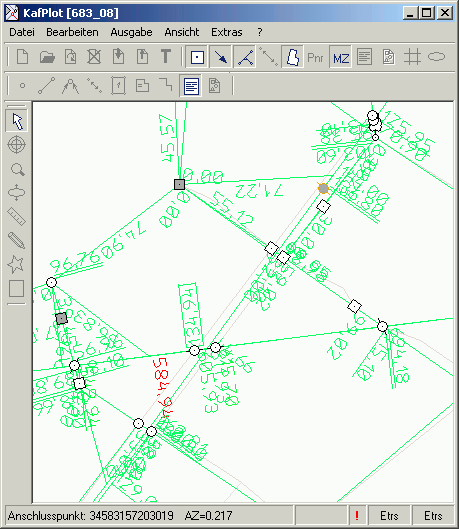
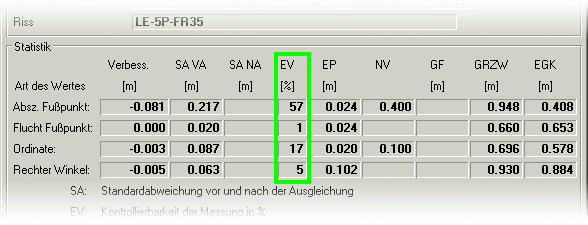
Kontrollierbarkeit EV
Der Kennwert Kontrollierbarkeit EV zeigt an, wie gut die Beobachtung durch die Messungskonfiguration kontrolliert ist.
Er wird in Prozent angegeben und errechnet sich aus dem Redundanzanteil multipliziert mit 100.
Die Kontrollierbarkeit
Die sich aus der Ausgleichung ergebende Kontrollierbarkeit protokolliert KAFKA in der Ausgabedatei LT2.
In den Steuerzeilen kann mit dem Wert IGEV ein Grenzwert festgelegt werden, bis zu dem
eine Beobachtung als nicht kontrolliert gelten soll. Beobachtungen die eine kleinere Kontrollierbarkeit besitzen, werden in der
Ausgabedatei LT2 mit "--N.K.--" als nicht kontrolliert ausgewiesen. Soweit das Lesen der Datei LT2 nicht abgeschalten ist,
liest KafPlot daraus die Standardabweichungen und ordnet sie dem Messwert zu.
Folgende Aussagen können anhand des Wertes EV getroffen werden:
| 0% | - | 5% | unkontrolliert |
| 5% | - | 10% | schlecht kontrolliert |
| 10% | - | 30% | ausreichend kontrolliert |
| 30% | - | 70% | kontrolliert |
| 70% | - | 100% | gut kontrolliert |
Die Kontrollierbarkeit ist neben der Beobachtungskonfiguration auch abhängig von den Standardabweichungen SA VA
der Beobachtungen. Die präziseren Beobachtungen kontrollieren die weniger präzisen Beobachtungen stärker als umgekehrt.
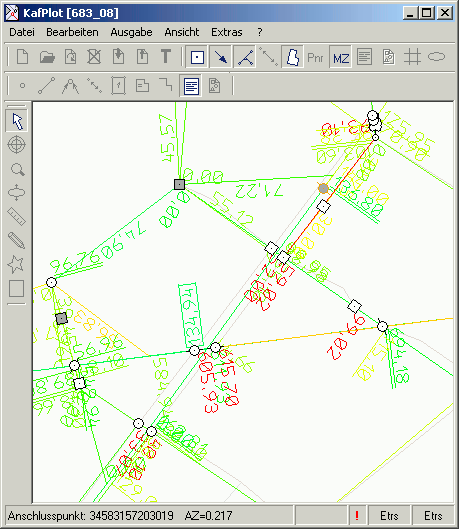
Die Anzeige der Kontrollierbarkeit
In hochwertigen Lagenetzen sollte auf eine hohe Kontrollierbarkeit aller Beobachtungen Wert gelegt werden. Diese
kann in der Regel nur durch die Einschaltung zusätzlicher Beobachtungen erhöht werden. Bei der Auswertung von Katasternachweis
ist man auf das zur Verfügung stehende Zahlenmaterial beschränkt.
Bei schlechter Kontrollierbarkeit können grobe Fehler im Zahlenmaterial kaum erkannt werden. Dies schlägt sich besonders in dem Einfluss auf die
Punktlage EP, im Grenzwert der Fehlererkennbarkeit GRZW und in dem Einfluss eines nicht
erkannten groben Fehlers EGK nieder. Soweit von der Ausgleichung grobe Fehler erkannt werden, ist die tatsächliche
Fehlerursache dann selten eingrenzbar. Nur eine örtliche Messung, also das Einführen von weiteren Beobachtungen kann dann weiter helfen.
Übertrifft EV den Wert 100%, dann liegt ein Konfigurationsdefekt vor, das Datenmaterial muß geprüft werden. Es gibt
z.B. lokale Unterbestimmungen aufgrund fehlender PNR-Eingabe für einen Lotfußpunkt, der an anderer Stelle nummeriert ist. Der Grund für einen
Konfigurationsdefekt könnte beispielsweise auch in der simultanen Verarbeitung zweier Netzteile liegen, die durch keinerlei Messungen miteinander
verbunden sind.
Der Kennwert EV gibt an, wie gut eine Beobachtung durch andere kontrolliert ist. Hiermit ist ein Maß für die innere Zuverlässigkeit der Messungskonfiguration gegeben.
Ein schlechter EV-Wert schränkt die Erkennbarkeit von groben Fehlern wesentlich ein.
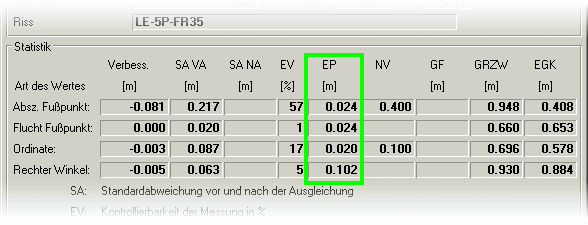
Einfluss der Beobachtung auf die relative Punktlage EP
Die Kenngröße EP beschreibt den Einfluss der Beobachtung auf die relative Punktlage. Die anhängenden Punkte würden sich um diesen Betrag verschieben, wenn
die betreffende Beobachtung nicht an der Ausgleichung teilnimmt.
Der Einfluss auf die Punktlage
Den sich aus der Ausgleichung ergebende Wert EP protokolliert KAFKA in der Ausgabedatei LT2. KafPlot liest diesen und ordnet ihm die
jeweilige Beobachtung zu.
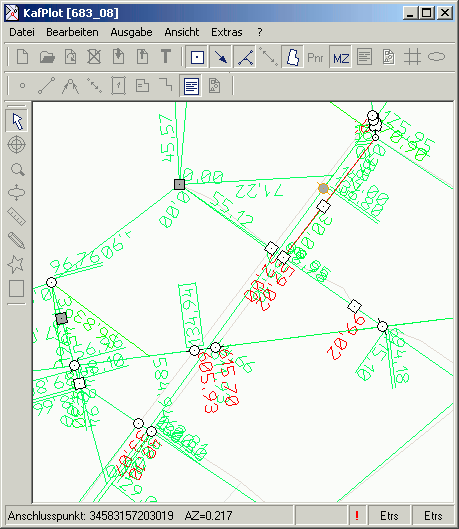
Die Anzeige des Einflusses auf die Punktlage
In der Kenngröße EP ist die äußere Zuverlässigkeit der Messungs- und Netzkonfiguration festgehalten.
Große EP-Werte deuten auf die Unverzichtbarkeit der einzelnen Beobachtungen hin, bedeuten damit aber auch, dass ein grober Fehler kaum
aufgedeckt werden kann. Ziel muss es also sein, den EP-Wert möglichs klein zu halten.
Die Kenngröße EP gibt den Einfluss der Beobachtung auf die relative Punktlage an. Die Punkte würden sich um diesen Betrag verschieben, wenn die
Beobachtung ausgeschaltet würde.
Normierte Verbesserung NV
Die Normierte Verbesserung NV ist die wichtigste Kenngröße bei der Untersuchung des Datenmaterials nach groben Fehlern.
Es ist eine dimensionslose Größe.
In die Berechnung der normierten Verbesserung fließen die Standardabweichung SA VA, die Verbesserung V und die
Kontrollierbarkeit EV ein. Bei geringer Kontrollierbarkeit einer Beobachtung wird im Regelfall ein kleiner NV-Wert entstehen,
auch wenn ein grober Fehler vorliegt. Ein grober Fehler kann dann nicht aufgedeckt werden.

Die Normierte Verbesserung
Den sich aus der Ausgleichung ergebende Wert NV protokolliert KAFKA in der Ausgabedatei LT2. KafPlot liest diesen und ordnet ihn der
Beobachtung zu. In den Steuerzeilen kann der Grenzwert k angegeben werden, der mit 3.3 voreingestellt ist. Beobachtungen,
bei denen der NV-Wert den Grenzwert k überschreitet, werden in dem Ausgabeprotokoll LT2 als grober Fehler markiert. Für diese Beobachtungen wird dann auch die
Größe des vermutlichen groben Fehlers GF errechnet.
Zusätzlich werden Beobachtungen mit einer hohen Normierten Verbesserung in dem Fehlerprotokoll LT6 ausgegeben, hier sortiert nach größten NV-Werten.
Das Lesen dieser Protokolldatei kann unter KafPlot zugeschalten werden, es werden für jeden Fehler Meldungsfenster angezeigt.
Folgende Aussagen können anhand des Wertes NV getroffen werden:
| 0.0 | - | 2.6 | vermutlich kein grober Fehler |
| 2.6 | - | 3.3 | vermutlich grober Fehler |
| 3.3 | - | 4.1 | grober Fehler wahrscheinlich |
Bei Auswertungen mit hohen Anforderungen an die Zuverlässigkeit, wie z.B. Festpunktfelder, sollte der Grenzwert k auf etwa 2.6 eingestellt werden.
An Auswertungen, an die nicht so hohe Anforderungen bezüglich der Zuverlässigkeit gestellt werden können, kann der Grenzwert k bis auf 4.1 gesetzt werden.
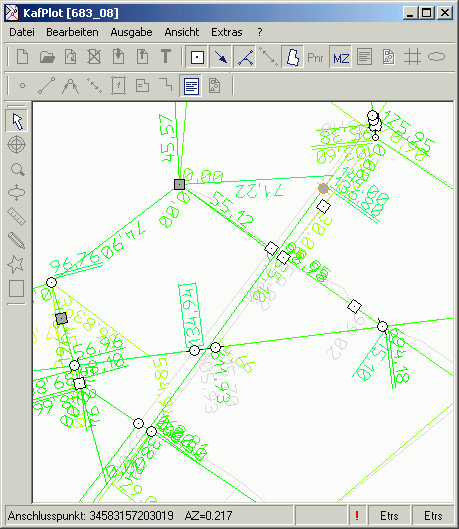
Die Anzeige der Normierten Verbesserung
Zu beachten ist, dass gerade bei gering kontrollierten Beobachtungen eventuelle grobe Fehler in die Nachbarschaft verschmieren. Damit
wird dann auch ein zu geringer NV-Wert ausgegeben und der Test auf grobe Fehler scheitert. Wenn in der KafPlotGrafik ersichtlich ist, dass mehrere Messungen
mit einem erhöhten NV-Wert entstehen, sollten die Beobachtungen mit den größten NV-Werten gesondert untersucht werden. Im Regelfall hilft auch ein KAFKA-Rechenlauf
mit eingeschaltener robusten Schätzung (Startoption -R), einen groben Fehler zu finden. KAFKA schaltet dann schrittweise mit jeder Iteration
die Beobachtungen mit erhöhten NV-Werten stochastisch ab. Der Verschmierungseffekt tritt dann nicht auf. Anhand der NV- und GF-Werte
ist dann ein wesentlich sicheres Auffinden wahrscheinlicher grober Fehler möglich.
Der errechnete Wert der Normierten Verbesserung ist abhängig von der eingehenden Standardabweichung SA VA.
Wenn bei ganzen Beobachtungsgruppen (Riss) erhöhte NV-Werte auch bei der robusten Schätzung entstehen, ist die Ursache in einer zu positiven Schätzung
der Standardabweichungen zu suchen. Wenn die Ursache der geringeren Genauigkeit der Beobachtungen erklärbar ist, kann die Beobachtungsgruppe herabgewichtet werden.
Die Normierten Verbesserung NV zeigt dem Anwender auf, wie kritisch die entstehende Verbesserung zu werten ist. Wird der Grenzwert 3.3 überschritten,
ist ein grober Fehler in der Beobachtung wahrscheinlich.
Geschätzter grober Fehler GF
Sobald ein kritischer Wert für die normierte Verbesserung NV erreicht ist, gibt GF die Größe des vermutlichen groben Fehlers an.
Der grobe Fehler hat naturgemäß ein umgekehrtes Vorzeichen zur Verbesserung. Sein Betrag kann Meterfehler, Eingabefehler, gon-Fehler
oder Punktverwechselungen schnell aufzudecken helfen.

Der geschätzte grobe Fehler
Sobald ein kritischer NV-Wert auftritt, gibt KAFKA für die Beobachtungskomponente den geschätzen groben Fehler
in der LT2-Protokolldatei an. Im Protokoll wird der Fehler in der Dimension des Beobachtungswertes angegeben. KafPlot rechnet wie schon
bei der Verbesserung V und der Standardabweichung SA VA den Messwert in Meter um.
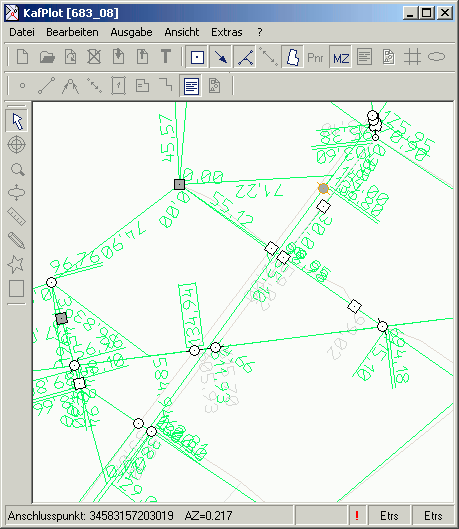
Die Anzeige des vermutlichen groben Fehlers
Wie schon bei der normierten Verbesserung NV bemerkt, wirken sich grobe Fehler bei der vermittelnden Ausgleichung
auch auf die benachbarten Beobachtungen aus. Eine bessere Schätzung des vermutlichen groben Fehlers erhält man, wenn beim Rechenlauf
die Robuste Schätzung (Startoption -R) eingeschaltet wird.
Der Kennwert GF gibt die Größe eines vermuteten groben Fehlers an.
Grenzwert der Erkennbarkeit eines groben Fehlers GRZW
Der Kennwert GRZW gibt an, wie groß eine Verbesserung werden kann, ehe sie als grober Fehler erkannt wird.

Der Grenzwert der Erkennbarkeit eines groben Fehlers
Der Kennwert GRZW ergibt sich aus der vorgegebenen Genauigkeit SA VA, der Kontrolliertheit EV
und dem Grenzwert k der normierten Verbesserung NV (in der Regel 3.3). KafPlot berechnet die Größe anhand der aus der LT2-Datei gelesenen
statistischen Werte der Beobachtung.
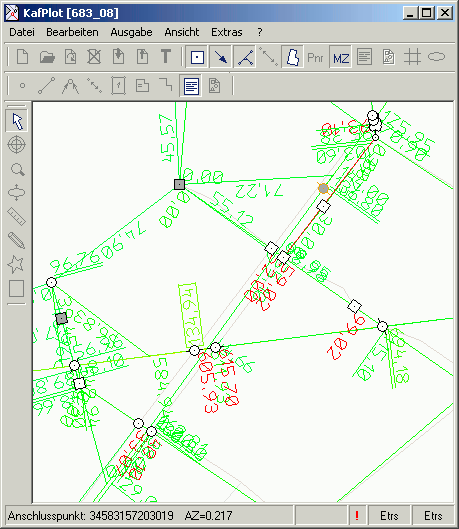
Die Anzeige der Erkennbarkeit eines groben Fehlers
Grobe Fehler in den Beobachtungen werden anhand der normierten Verbesserung NV erkannt. Wenn der NV-Wert einer Beobachtung den
Grenzwert k (in der Regel 3.3) überschritten hat, wird sie als grober Fehler markiert. Der Kennwert GRZW gibt an, wie groß die Verbesserung einer Beobachtung
sein muss, damit der NV-Wert gerade den Grenzwert k erreicht. Je schlechter die Standardabweichung SA VA und je kleiner die Kontrollierbarkeit EV
einer Beobachtung ist, desto schlechter sind grobe Fehler erkennbar. Das schlägt sich in der Kenngröße GRZW nieder.
Die Kenngröße GRZW einer Beobachtung gibt an, ab welcher Verbesserung ein grober Fehler erkannt werden würde. Sie ist ein Maß der inneren Zuverlässigkeit der Messungskonfiguration.
Einfluss eines nicht erkannten groben Fehlers EGK
Die Kenngröße EGK ist ein Maß der äußeren Zuverlässigkeit, das sich auf eine Beobachtung bezieht. Diese Größe gibt an, wie stark sich ein nicht
mehr erkennbarer grober Fehler GRZW einer Beobachtung auf die Koordinaten der anhängenden Punkte auswirkt.

Der Einfluss eines nicht erkennbaren groben Fehlers
Die Größe EGK berechnet sich aus dem Grenzwert der Fehlererkennbarkeit GRZW und der Kontrollierbarkeit EV einer Beobachtung.
KafPlot berechnet diesen Wert anhand der aus der LT2-Datei gelesenenen statistischen Werte der Beobachtung.
Die Anzeige des Einflusses eines groben Fehlers
Die Kenngröße EGK gibt an, wie groß die Auswirkung eines nicht erkannten groben Fehlers auf die anhängenden Punkte ist. Je besser
eine Beobachtung durch andere Beobachtungen kontrolliert ist, desto kleiner ist der Einfluss eines groben Fehlers auf die Punktlage. Dagegen wirkt sich
ein grober Fehler einer schlecht kontrollierten Beobachtung voll auf die Koordinaten der anhängenden Punkte aus.
Der Wert EGK ist ein relatives Maß bezüglich der an der Beobachtung hängenden Punkte. Inwieweit sich ein nicht erkannter grober Fehler global auf das
Punktfeld auswirkt, ist nicht bestimmbar. Gerade bei schwach kontrolliertem Katasternachweis kann sich die Wirkung eines nicht erkannten groben Fehlers auf
weitaus mehr Punkte ausdehnen. Der Einfluss lässt sich nur durch ausreichend Passpunkte begrenzen.
Die Kenngröße EGK gibt an, wie groß die Auswirkung eines nicht erkannten groben Fehlers auf die anhängenden Punkte ist. Sie ist ein Maß der äußeren
Zuverlässigkeit der Messungskonfiguration.
 KafPlot-Support (Info, Fragen, Anregungen)
KafPlot-Support (Info, Fragen, Anregungen)

 Einleitung
Einleitung Punkte
Punkte Koordinatenverschiebung dy, dx und ds
Koordinatenverschiebung dy, dx und ds Standardabweichung SP, Fehlerellipse a, b und t
Standardabweichung SP, Fehlerellipse a, b und t Lokale Standardabweichung LSP
Lokale Standardabweichung LSP Punktzuverlässigkeit ZL
Punktzuverlässigkeit ZL Anschlussgenauigkeit AG und -zuverlässigkeit AZ
Anschlussgenauigkeit AG und -zuverlässigkeit AZ Beobachtungen
Beobachtungen Verbesserung V
Verbesserung V Standardabweichung SAV
Standardabweichung SAV Standardabweichung SAN
Standardabweichung SAN Kontrollierbarkeit EV
Kontrollierbarkeit EV Einfluss auf die Punktlage EP
Einfluss auf die Punktlage EP Normierte Verbesserung NV
Normierte Verbesserung NV Geschätzter grober Fehler GF
Geschätzter grober Fehler GF Grenzwert der Fehlererkennbarkeit GRZW
Grenzwert der Fehlererkennbarkeit GRZW Einfluss eines nicht erkannten groben Fehlers EGK
Einfluss eines nicht erkannten groben Fehlers EGK
 anzuschalten. Unter Ansicht > Optionen > Punkte > Fehlerdarstellung ist der
gewünschte Kennwert anzuwählen. Der Wert wird dann als rote Linie, Ellipse oder Kreis präsentiert. Mit dem
anzuschalten. Unter Ansicht > Optionen > Punkte > Fehlerdarstellung ist der
gewünschte Kennwert anzuwählen. Der Wert wird dann als rote Linie, Ellipse oder Kreis präsentiert. Mit dem 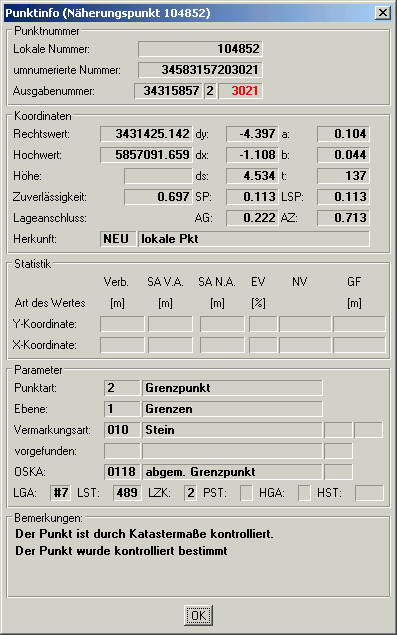
 Die Felder dy und dx bei einem Neupunkt
Die Felder dy und dx bei einem Neupunkt Die Felder dy und dx bei einem beweglichen Anschlusspunkt
Die Felder dy und dx bei einem beweglichen Anschlusspunkt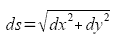
 Die vektorielle Anzeige der Punktverschiebung
Die vektorielle Anzeige der Punktverschiebung Die Hotspot-Anzeige der Punktverschiebung
Die Hotspot-Anzeige der Punktverschiebung
 Die Komponenten der Fehlerellipse und die Standardabweichung
Die Komponenten der Fehlerellipse und die Standardabweichung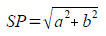
 Die Anzeige der Fehlerellipsen
Die Anzeige der Fehlerellipsen Die Hotspot-Anzeige der Standardabweichung
Die Hotspot-Anzeige der Standardabweichung Die lokale Standardabweichung
Die lokale Standardabweichung Die Punktzuverlässigkeit
Die Punktzuverlässigkeit Die Anzeige der Zuverlässigkeit
Die Anzeige der Zuverlässigkeit Die Hotspot-Anzeige der Zuverlässigkeit
Die Hotspot-Anzeige der Zuverlässigkeit Die Anschlussgenauigkeit und -zuverlässigkeit
Die Anschlussgenauigkeit und -zuverlässigkeit Die Anzeige der Anschlussgenauigkeit
Die Anzeige der Anschlussgenauigkeit Die Hotspot-Anzeige der Anschlussgenauigkeit
Die Hotspot-Anzeige der Anschlussgenauigkeit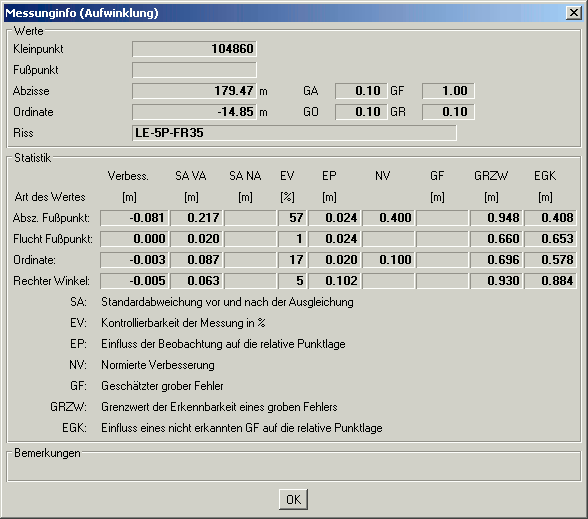
 Die Verbesserung
Die Verbesserung Die Anzeige der Verbesserungen
Die Anzeige der Verbesserungen Die Standardabweichung vor der Ausgleichung
Die Standardabweichung vor der Ausgleichung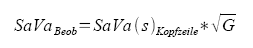
 Die Anzeige der Standardabweichungen
Die Anzeige der Standardabweichungen Die Standardabweichung nach der Ausgleichung
Die Standardabweichung nach der Ausgleichung Die Anzeige der Differenz V - SA VA
Die Anzeige der Differenz V - SA VA Die Kontrollierbarkeit
Die Kontrollierbarkeit Die Anzeige der Kontrollierbarkeit
Die Anzeige der Kontrollierbarkeit Der Einfluss auf die Punktlage
Der Einfluss auf die Punktlage Die Anzeige des Einflusses auf die Punktlage
Die Anzeige des Einflusses auf die Punktlage Die Normierte Verbesserung
Die Normierte Verbesserung Die Anzeige der Normierten Verbesserung
Die Anzeige der Normierten Verbesserung Der geschätzte grobe Fehler
Der geschätzte grobe Fehler Die Anzeige des vermutlichen groben Fehlers
Die Anzeige des vermutlichen groben Fehlers Der Grenzwert der Erkennbarkeit eines groben Fehlers
Der Grenzwert der Erkennbarkeit eines groben Fehlers Die Anzeige der Erkennbarkeit eines groben Fehlers
Die Anzeige der Erkennbarkeit eines groben Fehlers Der Einfluss eines nicht erkennbaren groben Fehlers
Der Einfluss eines nicht erkennbaren groben Fehlers Die Anzeige des Einflusses eines groben Fehlers
Die Anzeige des Einflusses eines groben Fehlers